
こんにちは。作業療法士Sです。
作業療法研究法に関する内容も今回で7記事目、今回から統計関連について書いていこうと思います。
今回は2変数のパラメトリック検定について書いていきます。
統計処理:パラメトリック検定
正規分布する2変数を扱う場合
 作業療法士S
作業療法士S平均値が使える時はパラメトリック検定を用います。
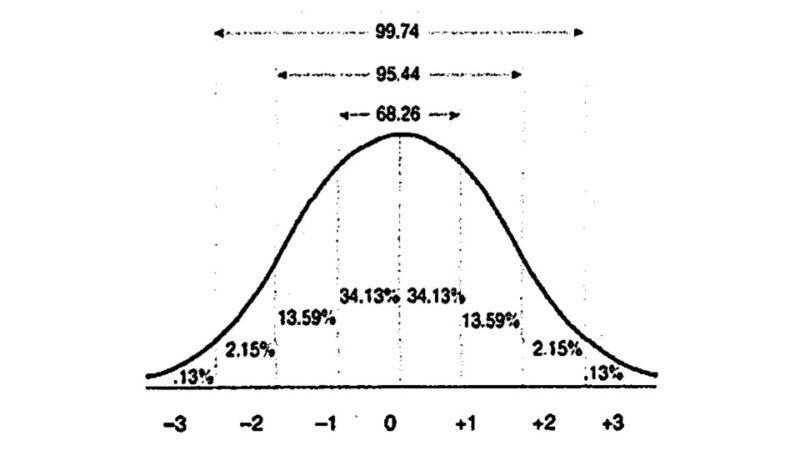
測定した2変数が正規分布する場合、分散を推論することができる
 作業療法士S
作業療法士S平均値は分散を代表する値です。
手順の確認
手順 ①
対象群の媒介変数を用いて、研究疑問を立案する
手順 ②
研究疑問を2つの仮説に翻訳する
無効の仮説:null hypothesis
選択する仮説:alternative hypothesis
手順 ③
仮説Hαが1方向か、2方向かを決める(片側か両側か)
 作業療法士S
作業療法士S1方向は < >の仮説で片側、
2方向は ≠の仮説で両側です。
手順 ④
有意差(α)レベルを設定する、αはエラーが生じる可能性を表す
 作業療法士S
作業療法士S通常は0.05であり、αレベル=0.05と表します。α=0.01の場合は一層厳密になります。
無効の仮説が正しいにもかかわらず、仮説を棄却する可能性がどれくらいかということです。
検査者が間違って真実の可能性を黙殺する可能性が5%(20回に1回)
95%正しい「確からしさ」
手順 ⑤
データ収集と検証に進む
手順 ⑥
検証した統計の値をPの価(プロパビリティ、可能性)に変更する
 作業療法士S
作業療法士Sこれがデータが示した実際の測定値、尺度、頻度の平均値から全体を推論する確からしさの割合です。
(この割合はH0やサンプルサイズに影響されます。)
手順 ⑦
Pの価がαレベルより小さい:H0を棄却して(有意な結果)、Hαを採択する。
Pの価がαレベルより大きい:H0を採択する(有意でない結果)、Hαは採択されない。
2つのパラメトリック検定
 作業療法士S
作業療法士Sパラメトリック検定には、
対応のあるパラメトリック検定、対応のないパラメトリック検定
があります。
Paired T Test
Group T Test
Paired T Test
- 対応のあるT検定テスト
- 2つの集団の変数が正規分布するとき、対応のある変数間の平均値により差の有無を分布により推論することができる
- 対応のある変数
例題
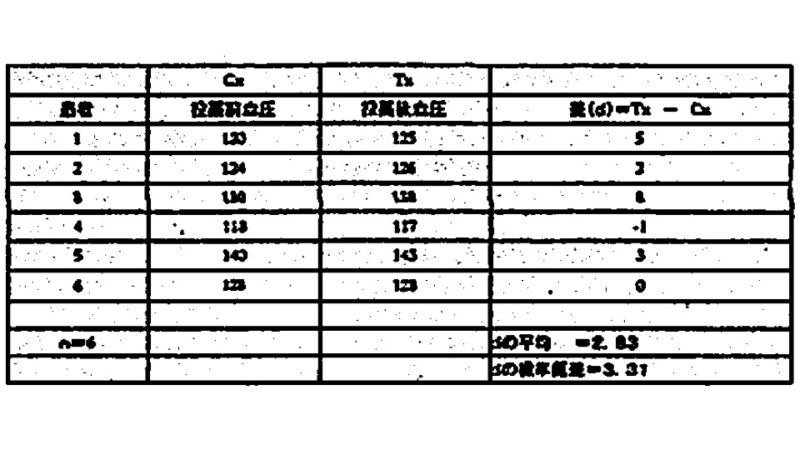
ある薬の血圧増加効果について治験がなされた。
6名の男性患者が、投薬前と投薬後の血圧測定を受けて、その価を上記に記す。(単位はmmHg)
これらのデータは投薬による血圧の増加を示すと考えて良いか。
μT -μC=血圧における差の平均値
H0:μT -μC=0 投薬前後の差はない
Hα:μTーμC>0 投薬後は投薬前に比べて増加している
αレベル=0.05 片側検定 one-sided
Tの値 {(2.83-0)×√6 }÷3.31=2.09
…(血圧の差の平均値ー差)×サンプル数の平方根を差の標準偏差で割ったもの
自由度(degree of freedom) df=6-1=5
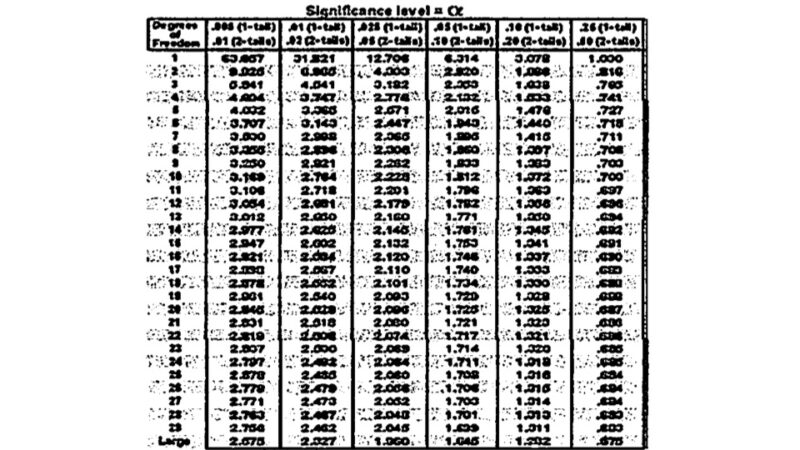

T=2.09であり、表からp=0.05のTの値よりも小さく、p=0.025の値よりも大きい
このことより、データから導かれたpの値は0.05よりも小さいことがわかる
ある薬の血圧増加効果について治験がなされた。
6名の男性患者が、投薬前と投薬後の血圧測定を受けて、その価を上記に記す。(単位はmmHg)
これらのデータは投薬による血圧の増加を示すと考えて良いか。
↓
治験結果のデータは投薬前と投薬後の平均血圧には、統計的な有意な上昇が認められるということを示している。(p<0.05)
Group T Test
- 対応のないT検定テスト
- 2つの集団の変数が正規分布するが、対応がなく大きさの異なる集団の平均値から変数間の差の有無を分布により推論する
- 対応のない変数
 作業療法士S
作業療法士S教科書には、ウェルチのTテストと説明されていることが多いです。
例題
| Tx(治療) | Cx(コントロール) | ||
| 誘発分娩群 | 自然分娩群 | サンプル数 111+117=228 | |
| サンプル数 | 111人 | 117人 | df:228-2=226 |
| 失血平均量 | 185cc | 233cc | |
| 失血標準偏差 | 139cc | 150cc |
ランダム化された実験で、
111名が妊娠39週から40週まで誘発分娩を選択的に実施され、比較対照群として117名が妊娠41週での自然分娩を受けた。すべてのサンプルが分娩後の失血について測定を受け、以上の結果を示した。
2つのグループに差があるか。
μT -μC=群の平均失血量における差
H0:μT -μC=0 誘発群と自然群の差はない
Hα:μTーμC≠0 誘発群は自然群には差がある
αレベル=0.05 両側検定 two-sided
両群のデータを合わせて推定することで推定精度を良くする、データを集めて分散から推定する。
プールされた分散:{(111-1)×1392+(117-1)×1502 }÷(111+117-2)≒20952
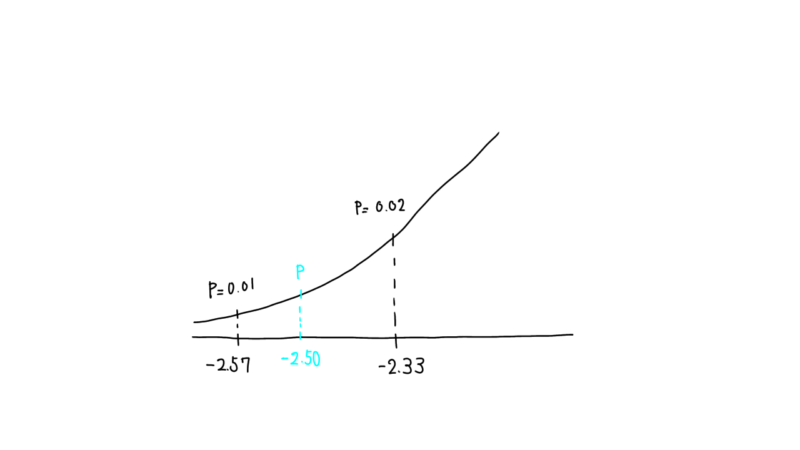
Tの値 [{(185-233)-0 }÷√20952 ]×(1/117+1/111)=-2.50
自由度(degree of freedom) df=111+117-2=226

ランダム化された実験で、
111名が妊娠39週から40週まで誘発分娩を選択的に実施され、比較対照群として117名が妊娠41週での自然分娩を受けた。すべてのサンプルが分娩後の失血について測定を受け、以上の結果を示した。
2つのグループに差があるか。
↓
治験結果のデータから、誘発分娩群と自然分娩群の平均出血量には統計的な有意な差が認められるということを示している(p<0.02)
まとめ
今回は2変数のパラメトリック検定について書いていきました。
測定した2変数が正規分布する場合は測定結果を平均して議論することができたり、分散を推論することができます。
対応の有無(同じサンプル群or違うサンプル群)、7つの手順に則り検定を行なっていきましょう。

