こんにちは。作業療法士Sです。
前回の記事では、２変数のパラメトリック検定について書いていきました。
今回は２変数のノンパラメトリック検定について書いていこうと思います。
統計処理：ノンパラメトリック検定
正規分布しない２変数を扱う場合
作業療法士S平均値を使うことができない時はノンパラメトリック検定を用います。
測定した２変数が正規分布しない場合、分散を推論することができない
作業療法士Sそのため、ランキング（順位付け）を用います。
平均値で推論せず、中央値（median）で推論します。
2つのノンパラメトリック検定
作業療法士Sノンパラメトリック検定には、
対応のあるノンパラメトリック検定、対応のないノンパラメトリック検定
があります。
ウィルコクソン符号順位検定
Wilcoxon signed-rank test
ウィルコクソン順位和検定
Wilcoxon rank sum test
ウィルコクソン符号順位検定
- 対応のあるTテストを正規分布しないサンプルに当てはめたもの
手順 ①
処理（治療）前と後の差を導き出し、順位付けを行う
作業療法士Sこの時には＋,−は無視します。
変数の値は関係ありません！
手順 ②
差がないもの（d＝0）はまとめてランクから外す
作業療法士S自動的にサンプル数は減っていきます。
手順 ③
差が同じものは、ランキングの順位を同じにする
作業療法士Sランキングの平均値を与えます。
手順 ④
差の＋，−を元に戻して計算する （T＋＝＋のランクの総和 T -＝ -ランクの総和）
手順 ⑤
測定値の小さいものから大きいものへ並び替える
手順 ⑥
総数n個のサンプルに1からnまでランキングをつける
手順 ⑦
同じものは、ランキングの順位を同じにする
作業療法士Sランキングの平均値を与えます。
手順 ⑧
小さなグループのランキングを合計したものをT1とする
手順 ⑨
表による2サイド（両側の、差が≠である）の基準値を求める
手順 ⑩
もしT＋（あるいはT -）が数値の範囲内であれば、H0を受け入れる
（H0とは差がない、変化がない、変わりないとする仮説）
もしT＋（あるいはT -）が数値の範囲内でなければ、H0を棄却して、Hαを受け入れる
（Hαとは差がある、変化があるとする仮説）
ウィルコクソン符号順位検定 例題
| 犬 | 治療前 | 治療後 | 差 | ランク | サインランク |
| 1 | 125 | 69 | 56 | 12 | 12 |
| 2 | 52 | 82 | -30 | 4 | -4 |
| 3 | 91 | 37 | 54 | 11 | 11 |
| 4 | 97 | 58 | 39 | 7 | 7 |
| 5 | 82 | 30 | 52 | 10 | 10 |
| 6 | 53 | 33 | 20 | 3 | 3 |
| 7 | 71 | 71 | 0（削除） | – | – |
| 8 | 128 | 82 | 46 | 8 | 8 |
| 9 | 71 | 84 | -13 | 1 | -1 |
| 10 | 63 | 30 | 33 | 5.5 | 5.5 |
| 11 | 66 | 47 | 19 | 2 | 2 |
| 12 | 107 | 38 | 69 | 13 | 13 |
| 13 | 144 | 95 | 49 | 9 | 9 |
| 14 | 106 | 73 | 33 | 5.5 | 5.5 |
Xを犬の左心臓側の血流量とする。（mg /100g単位で左静脈で測定した）
治療介入として心嚢部分にタンポンを留置し血流に影響を与えるかについて検証する。
TX：「心嚢」でのタンポナーデ
H0：タンポナーデによる影響はなかった（差の中央値は０である）
Hα：治療効果はあった（≠である）
サンプル数は13
T＋の絶対値86 T -の絶対値5
影響の有無であれば≠なので、両側検定
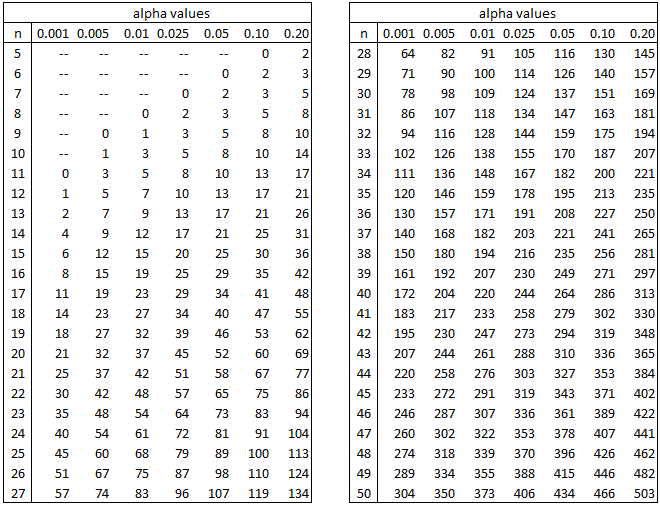
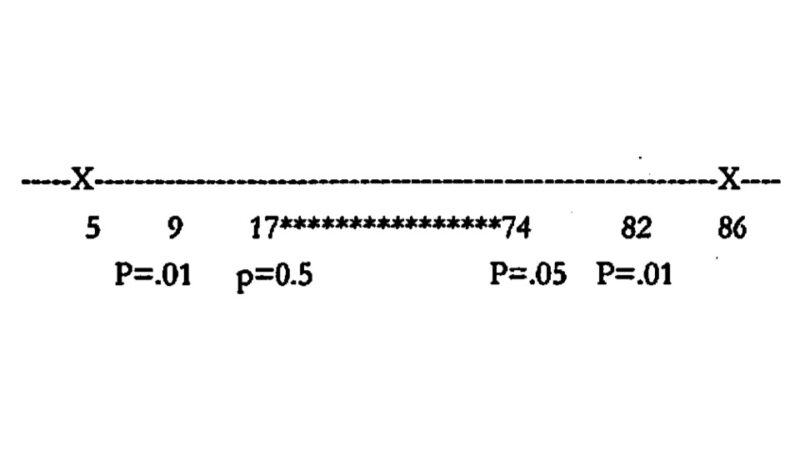
サンプル数13で上記の表を見ると、仮説を受ける範囲は
有意差0.01：9〜82（合計91）
有意差0.05：17〜74（合計91）
有意差0.025：13〜78（合計91）
仮説を受け入れる範囲は17〜74の間、今回の範囲は5〜86（X)のため超えている。
Xの位置を考えると、仮説を受け入れる範囲から離れているので、影響がないという仮説を棄却する。
犬の左心臓側の血流量は、治療介入として心嚢部分にタンポンを留置した場合、統計的に有意な影響を受ける。（p＜0.05）
ウィルコクソン順位和検定
- 対応のないTテストを正規分布しないサンプルに当てはめたもの
作業療法士S教科書には、マンホイットニーのU検定と書かれていることもあります。
手順 ①
測定値の小さいものから大きいものへ並び替える
手順 ②
総数n個のサンプルに1からnまでのランキングをつける
手順 ③
同じものは、ランキングの順位を同じにする
作業療法士Sランキングの平均値を与えます。
手順 ④
小さなグループのランキングを合計したものをT1とする
手順 ⑤
表による2サイド（両側の、≠がある）の標準値を求める
手順 ⑥
もし、T1が数値の範囲内であればH0を受け入れる
（H0とは差がない、変化がない、変わりないとする仮説）
もし、T1が数値の範囲外であればH0を棄却して、Hαを受け入れる
（Hαとは差がある、変化がある、変わりあるとする仮説）
ウィルコクソン順位和検定 例題
Xを24時間の尿サンプルから集められた総ヒステジンの排泄量とする。
以下の仮説を検証せよ。
データは男性5名（M）、女性10名（F）から
H0：男性と女性の中央値に差がない（差がない ＝）
Hα：男性と女性の中央値に差がある（差がある ≠）
| 男性 | 女性 |
| 229 | 197 |
| 236 | 224 |
| 435 | 115 |
| 172 | 135 |
| 432 | 74 |
| 138 | |
| 107 | |
| 204 | |
| 138 |
| 男性 | 女性 |
| 229 ⑫ | 197 ⑧ |
| 236 ⑬ | 224 ⑪ |
| 435 ⑮ | 115 ③ |
| 172 ⑦ | 135 ④ |
| 432 ⑭ | 74 ① |
| | 138 ⑤ |
| | 107 ② |
| | 204 ⑩ |
| | 138 ⑤ |
ランキングのデータ
男性：7、12、13、14、15
女性：1、2、3、4、5.5、5.5、8、9、10、11
n1（男性のグループのサンプル）＝5名
n2（女性のグループのサンプル）＝10名
T１＝7＋12＋13＋14＋15＝61
T２＝1＋2＋3＋4＋5.5＋5.5＋8＋9＋10＋11＝59
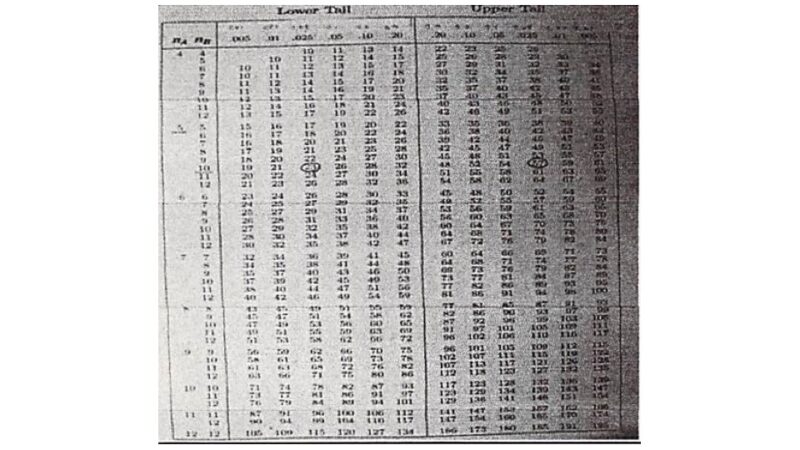
表より、下限から推測すると
仮説を受け入れる範囲は23〜57の間 （有意差0.05：23〜57）
Xの位置を考えると、仮説を受け入れる範囲から離れいているので、差がないという仮説を棄却する。
男性と女性のヒステジン排泄量の中央値には統計的に有意な差が認められる（p＜0.05）
まとめ
今回は、２変数のノンパラメトリック検定について書いていきました。
測定した２変数が正規分布しない場合は測定結果を平均して議論することができず、また分散を推論することができません。
ランキング（順位付け）を用いて、平均値で推論せず、中央値で推論していきましょう。